HSV to RGB integer conversion and the joy of reading techncial research

Recently, I have been obsessed with the idea of a game where you can breed different colored Pokemon, like those old creature simulators Grophland and Howrse. In the normal Pokemon games, you can’t have Pokemon with unique coat colors. Sometimes, there are color and regional variants, but those are limited to what is drawn by artists.

Could I simulate coat color breeding with simplified genetics? Maybe maybe, but let’s try something easier. I need to figure out how to generate randomly colored Pokemon. I don’t care if the colors look good or work well, I just need the ability to swap palettes first.

random_rgb(rattata)

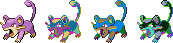
That was easy enough.

Onto the next step: parametrizing transformations between colors. I won’t be covering that in this post. This post is all about overcomplicating things and banging my head on the wall.

More importantly, I encountered a problem.

Sometimes, when converting an RGB color to HSV, and converting back, the RGB was different, just by a tiny bit. The hex code changed one letter. That’s not good. I immediately knew these were caused by floating point errors. Python’s built-in colorsys module uses float numbers, so indeed I had rounding errors.

In real life, randomness and mutations are inevitable, but for a game, and especially for a breeding mechanic, I don’t want unintentional randomness. The one thing that makes a game fun is that the game world isn’t as difficult as real life.

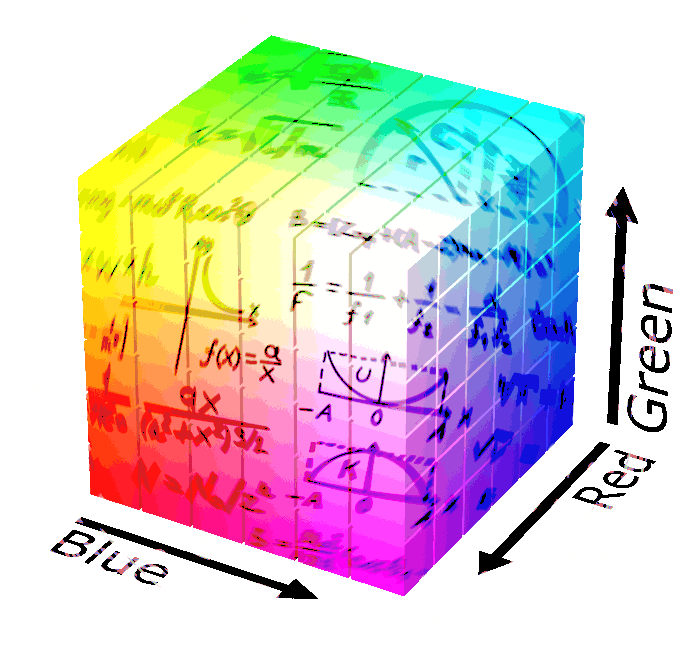
Why do I need to convert between RGB and HSV? Well, the RGB color system is meant for computer monitors. As humans, we don’t consider colors as a mix of red, green, blue. Hue Saturation Value (HSV) is easier to manipulate and conceptualize as pigments.

If I cannot rely on the colorsys module to do its job, then I need to figure out how to convert between RGB and HSV without any loss or errors. An internet search brought me to the research paper “Integer-Based Accurate Conversion between RGB and HSV Color Spaces” by Vladimir Chernov and co.

This looks promising! Since I am a degenerate who only knows how to copy and paste, I find the part that says, “The source code of all the tests can be found in the author’s repository [21]. The code is published under open source license.”

Hooray! I click on the link in the reference:

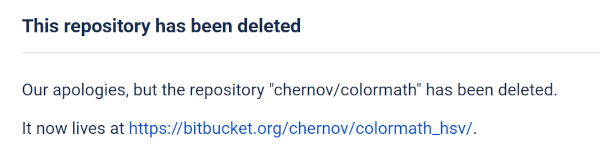
[21] Chernov Vladimir. Proposed algorithm source code; 2014. <https://bitbucket.org/chernov/colormath>

And… the repository is gone…

Well, no matter, the algorithm is written in the research paper. Nothing can possibly go wrong if I follow the 1-2-3 steps conveniently outlined by the researchers… right?

Right?

To convert RGV to HSV:

1. Find the maximum (M), minimum (m) and middle (c) of R, G, and B.

The middle?? What’s the middle of RGB? The average mean, or the median? Since RGB can be visualized as a coordinate in a 3D cube, does it mean the midpoint distance of the RGB vector?

Already, my efforts have gone wrong at the very first step. Nowhere in the paper is the defintion of middle mentioned.

The meaning of middling #

In Python and most programming languages, there are max([r,g,b]) and min([r,g,b]) functions which pick the biggest and smallest numbers of a set. Self-explanatory.

However there’s no mid([r,g,b]) function. I reread the paper, again, just to make sure I didn’t miss anything. The word “middle” only appears twice in the CTRL + F word search. Not many results for “mid” either. The closest to a human-like explanation is, “The middle component and sector offset are determined according to previously found maximum (M) and minimum (m).”

Yeah, no.

I opened a trusty search engine and entered terms like:

This search lead to some really strange answers: Bitwise XOR operator ^ to calculate middle in Java. (Ironically, this discussion contains the solution, but when I tried it, it didn’t work because the code was still incomplete. More on that later)

Ok, so, there’s no standard definition of middle. I’m on my own.

I got sidetracked and read some pages on bitwise shift operators because I cannot ever remember which side is right or left. I’m bad at directions.

Finally, I searched the author’s name and the missing repository: chernov colormath. Luckily for me, after scrolling down quite far, I found “How to calculate mid value of RGB image in matlab?”

The top answer by Walter Roberson contains a link to the source code by the authors of the paper.

He says that according to the code, the middle is just one of the R,G,B values. So if your red is 100, and your blue is 60, and your green is 20, then the middle is the blue value of 60. Red at 100 is the max, and green at 20 is the min. The last color is neither max nor min, hence, known as the “middle.” Wow. So simple.

Since the source code for the paper is still available online, I can finally port this algorithm into Python, right?

Right?

The RGB to HSV algorithm works fine. When I tried coding the backwards conversion from HSV to RGB, it doesn’t.

Documentation is a lie #

The Chernov paper claims that the algorithm works with no loss or errors. If this claim is true, my only recourse is to examine the source code and follow the implementation.

Long story short, where the research paper describes the steps, it is missing a step.

In math, every step has a corresponding inverse that also converts HSV back to RGB.

The backwards conversion formula was missing the reversal step, which caused the HSV to RGB formula to output incorrect results.

I examined their source code and derived the missing step:

if I == 1 or I == 3 or I == 5
  then F = E * (I + 1) - H

It should be performed at around step 5:

Unfotunately, it is not written out so plainly. It is hidden inside of a nest of if-statements.

I understand C++ is a different language, and the authors wanted to make their program as fast as possible. I also understand that English is not the authors’ native langauge, and I appreciate the work that has gone into the algorithm. It just hurts to read nested if-statements.

Anyway, with my newfound missing pieces, I implemented their HSV to RGB algorithm in Python:

E = 65537

def hsv_to_rgb(h, s, v) -> tuple[int, int int]:
    """Note that the hsv must be in the form given in the Chernov paper,
    which is ([0-393222], [0-65535], [0-255])
    NOT the typical ([0-359, [0-100], [0-100])"""
    
    delta = ((s * v) >> 16) + 1
    minimum = v - delta 

    if h < E:
        i=0
    elif h >= E and h < 2 * E:
        i=1
    elif h >= 2 * E and h < 3 * E:
        i=2
    elif h >= 3 * E and h < 4 * E:
        i=3
    elif h >= 4 * E and h < 5 * E:
        i=4
    else:
        i=5

    # The missing step: sector inversion inverse
    if i == 1 or i == 3 or i == 5:
        f = E * (i + 1) - h
    else:
        f = h - (E * i)

    mid = ((f * delta) >> 16) + minimum

    if i == 0:
        return v, mid, minimum
    elif i == 1:
        return mid, v, minimum
    elif i == 2:
        return minimum, v, mid
    elif i == 3:
        return minimum, mid, v
    elif i == 4:
        return mid, minimum, v
    else:
        return v, minimum, mid

The rest of my code can be found here.

In Python, you can write pseudocode almost word-for-word. You can write neat code in C++ too, but C++ programmers are a different breed.

Takeaways #

A combination of internet connection failures, either from my end or the BitBucket server, was a timesink. I rely on the internet sooooo much.

I learned a lot from trying to reproduce someone else’s research, and it requires the utmost of patience.

Would I have been able to figure out the missing step without the source code? Maybe if I stared at the paper long enough, I would compare the forward and backwards methods, and deduce that the reversal step was missing.

Or I might have to retrace everything, which means stepping into the authors’ shoes, adopt the mental model of 3 experts and acquire the same knowlege as them, figure out why they made certain decisions, how memory layouts work, how does overflow and integer division work, etc.

I don’t want to say that I’d just give up, but giving up is an option. I could just live with floating point rounding errors.

Maybe I’d continue Googling and searching, hoping someone else solved the problem in a similar fashion.

Could I have used ChatGPT to give me an algorithm?

Close, but no cigar. The “middle” refers to the median of my input RGB values.

Long story short, ChatGPT gave me an algorithm that was wrong, so it didn’t save time for me. Maybe if I was better at prompt writing, I’d get better results, but it’s already hard enough to write in a way that a human understands. How much harder is it to write something a robot can understand?

References #

Chernov, Vladimir, Jarmo Alander, and Vladimir Bochko. “Integer-Based Accurate Conversion between RGB and HSV Color Spaces.” Computers & Electrical Engineering 46, no. C (August 2015): 328–37. https://doi.org/10.1016/j.compeleceng.2015.08.005.